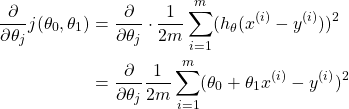Machine Learning : ตอนที่ 3

Technology by DrawassetLeave a Comment on Machine Learning : ตอนที่ 3

Machine Learning : ตอนที่ 3

Gradient Descent

จากบทความ Machine Learning ตอนที่2 ที่เราได้รู้จักสมการ Cost function และเป้าหมายของเราที่จะ Minimize Cost function j(\theta_{0},\theta_{1})ของเราแต่คำถามคือแล้วเราจะเริ่มต้นได้อย่างไร 

รูป 3.1 แสดง Contour plot ของ data training set

ลองนึกภาพการลงจากเขาเมื่อคุณอยู่ที่ตำแหน่งหนึ่งบนยอดเขา และเป้าหมายของเราคือมองไปรอบๆเพื่อหาทางที่สั้นที่สุดที่จะลงไปถึงหุบเขา เมื่อได้ทิศทางที่เห็นว่าสั้นที่สุดก็จะก้าวไปหนึ่งก้าว และหลังจากนั้นก็จะมองไปรอบๆอีกครั้งเพื่อหาทางที่จะก้าวต่อไปจนลงไปถึงบริเวณที่ต่ำที่สุด วิธีนี้เรียกว่า “Gradient Descent” ซึ่ง Gradient Descent ไม่ได้เพียงใช้หาค่า Minimize j(\theta_{0},\theta_{1}) ใน Linear Regression และยังสามารถใช้ในอัลกอริทึมอื่นๆที่จะกล่าวในบทความถัดไป

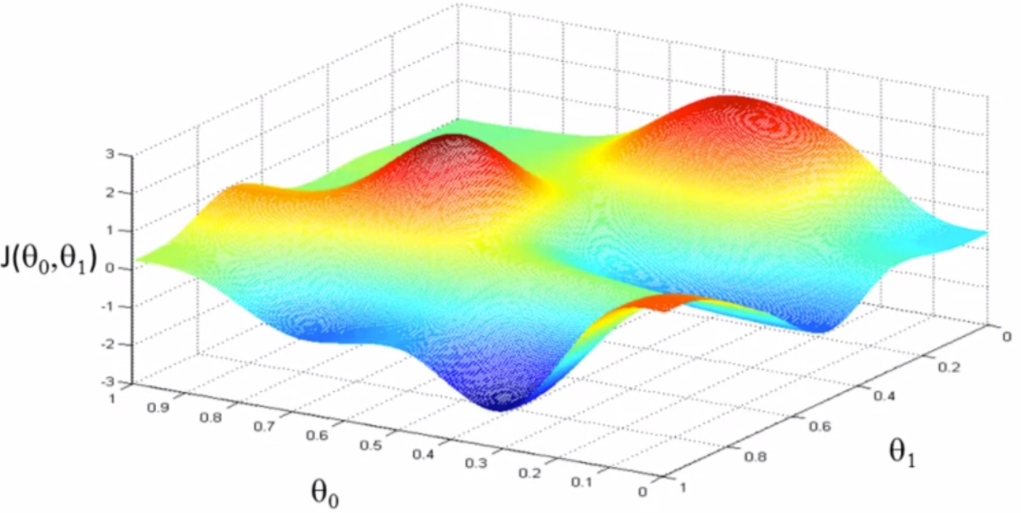
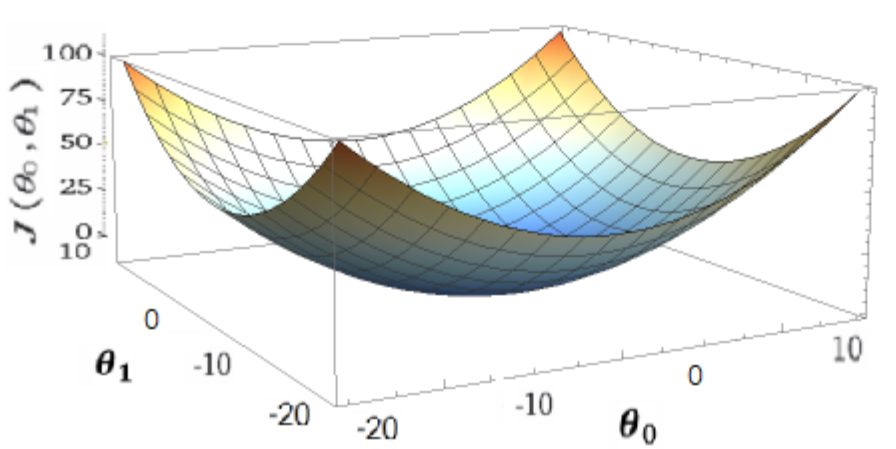
กลับมาที่เรื่อง training set ที่เรามี ก็เปรียบเสมือนกับภูเขาที่อาจจะมีเนินชันหรือไม่ชัน เส้นทางอาจจะซับซ้อนหรือไม่ซับซ้อน อาจจะมียอดเขาและหุบเขามากกว่าหนึ่งตำแหน่งและมีจุดที่ต่ำที่สุดเราจะเรียกว่า “Global Optimum” ส่วนหุบเขาในแต่ละตำแหน่งเราจะเรียกว่า “Local Optimum” ดังที่ได้แสดงในรูป 3.1 แต่ในกรณีที่ training set ของเราสามารถใช้อัลกอริทึม Linear Regression ได้แสดงว่า ข้อมูลของเรา เหมือนรูป 3.2 ซึ่งจะไม่มี local optimum มีเพียง global optimum เพียงตำแหน่งเดียว และยังแสดงว่าจุด Optimum ของ j(\theta_{0},\theta_{1}) มีเพียงจุดเดียว

รูป 3.2 แสดงภาพ Contour Plot แสดง ความชันของสมการ 2 ตัวแปร

เกริ่นกันมาพอสมควร ต่อไปเรามาดูสมาการและวิธีการหา Minimize j(\theta_{0},\theta_{1}) โดย Gradient Descent ว่าจะเริ่มต้นอย่างไร 

  1. กำหนดค่าเริ่มต้นของ0และ1 เช่น \theta_{0} = 0 และ \theta_{1} = 0
  2. เปลี่ยนค่า  \theta_{0} และ \theta_{1} เพื่อ ทำให้  j(\theta_{0},\theta_{1}) มีค่าลดลงไปเรื่อยๆจนถึงค่าลู่เข้า (Repeate until convergence) โดยการแทนค่าใหม่ของ \theta_{0} และ \theta_{1} ลงใน สมการ 3.1 ที่เป็นการนำเอาวิธี Gradient Descent ไปใช้หา Minimum ของ Cost funtion j(\theta_{0},\theta_{1})

    \[\theta_{่j} := \theta_{่j} - \alpha\frac{\partial}{\partial\theta_{j}}j(\theta_{0},\theta_{1}) ..........where....(j = 0 and j = 1 )............(3.1) \]

    \[\theta_{่0} := \theta_{่0} - \alpha\frac{\partial}{\partial\theta_{0}}j(\theta_{0}) ....................................(3.2)\]

    \[\theta_{่1} := \theta_{่1} - \alpha\frac{\partial}{\partial\theta_{1}}j(\theta_{1}) ....................................(3.3)\]

จากสมการ3.1 เรามาทำความเข้าใจหลักการทำงานของสมการ Gradient Descentกัน เริ่มต้นจากทางซ้ายตัว \theta_{่j} ในกรณีของเราคือ \theta_{0} และ \theta_{1} ซึ่งเราต้องอัพเดทค่า \theta_{่j} ทางซ้ายไปพร้อมๆกับทางขวาของเครื่องหมาย := เราเรียกว่า “Simultaneous update” โดยเราต้องคิด \theta_{0} และ \theta_{1} ที่ละตัวดังสมการ(3.2 และ 3.3) แต่อัพเดทค่าทั้งสองหลังจากที่คำนวณครบทั้งสองค่าแล้ว ถัดมาสัญลักษณ์ \alpha เรียกว่า “Learning rate” ซึ่งเป็นตัวที่กำหนดความเร็วในการ Train หรือ ถ้านึกถึงตัวอย่างข้างต้นเรื่องการเดินลงจากยอดเขา \alpha ก็ระยะห่างของก้าวแต่ละก้าว ถ้าค่า \alpha มาก ก้าวที่ก้าวก็จะใหญ่ที่จะเดินลงจากยอดเขา แต่ก็ไม่ใช่ว่ายิ่งเราใช้ค่า \alpha มากระบบของเราจะหาจุด Opimum ได้เร็วเพราะถ้าค่า \alpha มากเกินไปก็จะทำให้ระบบข้ามจุดที่ต่ำที่สุดไปได้นึกถึงการกระโดดไปมาบนปากหลุมแต่ลงไปไม่ได้เพราะก้าวใหญ่เกิน \alpha มากระบบของเราจะหาจุด Opimum ได้เร็วเพราะถ้าค่า \alpha มากเกินไปก็จะทำให้ระบบข้ามจุดที่ต่ำที่สุดไปได้นึกถึงการกระโดดไปมาบนปากหลุมแต่ลงไปไม่ได้เพราะก้าวใหญ่เกิน และก็ไม่ควรจะให้ค่าน้อยเกินไปเพราะจะทำให้ระบบของเราใช้เวลาการ Train ช้ามาก ซึ่งแม้ \alpha จะเป็นค่าคงที่แต่ก้าวแต่ละก้าวจะมีความห่างที่ไม่เท่ากัน จากรูปที่ 3.3A และ 3.3B ซึ่งก้าวที่เข้าใกล้จุด Optimum จะค่อยๆเล็กลงเรื่อยๆ จนถึงจุด convergence ก็จะได้จุด minimize ของ Squared error Cost function j(\theta_{0},\theta_{1})

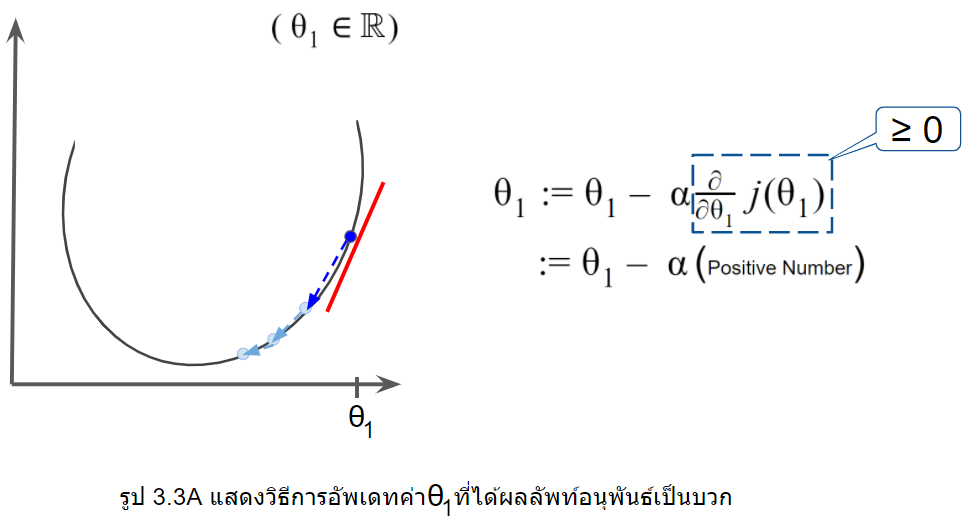
ถัดจาก \alpha คือส่วนของการอนุพันธ์ซึ่งจะเป็นส่วนสำคัญที่ทำให้ระบบรู้ว่าค่า  j(\theta_{0},\theta_{1}) ควรจะไปในทิศทางไหน จากรูป3.3A ให้ \theta_{1} เป็นสมาชิกของเลขจำนวนจริง (\theta_{1} \in \mathbb{R}) ในขณะที่ slope เส้นสีแดงของเราเป็นค่าบวก(positive number) ดังนั้นค่า \theta_{1} ก็จะลดลงเพราะค่า \theta_{1} ลบกับค่าบวกนั่นเอง

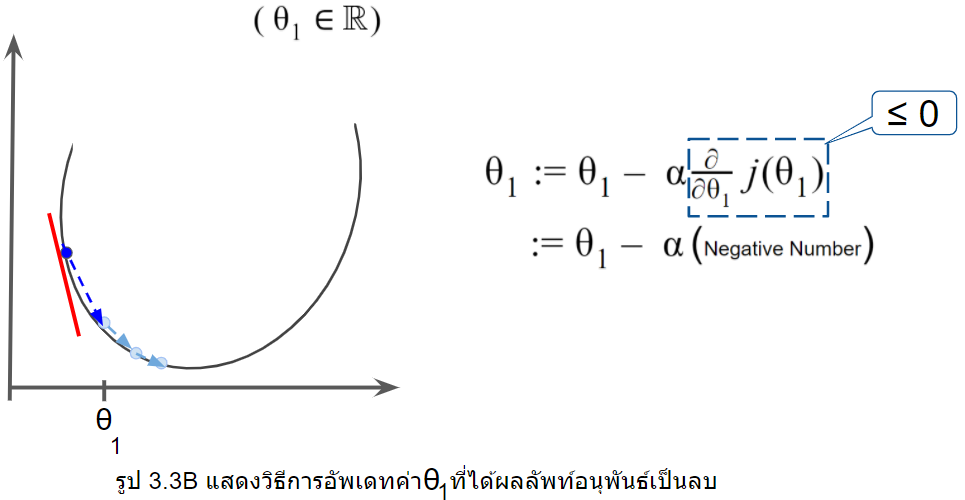
ในทางกลับกัน จากรูป3.3B ในขณะที่ slope เส้นสีแดงของเราเป็นค่าลบ(negative number) ดังนั้นค่า \theta_{1} ก็จะเพิ่มขึ้นเพราะค่า \theta_{1} ลบกับค่าลบ จึงกลายเป็นบวกกันนั่นเอง

    \[j(\theta_{0},\theta_{1}) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}-y^{(i)}))^{2}............................................(2.1)\]

จากบทความในตอนที่ 2 สมการที่ 2.1 Squared error Cost function นำมาแทนใส่ในสมการ 3.1 เราจะได้ดังนี้

 (1)    \begin{equation*}  \begin{split} \frac{\partial}{\partial\theta_{j}}j(\theta_{0},\theta_{1})  & = \frac{\partial}{\partial\theta_{j}} \cdot \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}-y^{(i)}))^{2} \\  & = \frac{\partial}{\partial\theta_{j}}・\frac{1}{2m}\sum_{i=1}^{m}(\theta_{0}+\theta_{1}x^{(i)}-y^{(i)})^{2} \end{split} \end{equation*}

ดังนั้นเมื่อ j=0 และ j=1 ลงในสมการและหาอนุพันธ์จะได้ผลลัพท์ดังนี้

 (2)    \begin{equation*}  j = 0 : \frac{\partial}{\partial\theta_{j}}j(\theta_{0},\theta_{1})  = \frac{1}{m} \cdot \sum_{i=1}^{m}(h_{\theta}(x^{(i)}-y^{(i)})) \end{equation*}


 (3)    \begin{equation*}  j = 1 : \frac{\partial}{\partial\theta_{j}}j(\theta_{0},\theta_{1})  = \frac{1}{m} \cdot \sum_{i=1}^{m}(h_{\theta}(x^{(i)}-y^{(i)})) \cdot x^{(i)} \end{equation*}

และเมื่อนำกลับไปแทนในสมการ3.2 และ สมการ3.3 จะได้

Repeat Until Convergence {

 (4)    \begin{equation*}  \theta_{0} := \theta_{0} - \alpha\frac{1}{m} \cdot \sum_{i=1}^{m}(h_{\theta}(x^{(i)}-y^{(i)})) \end{equation*}


 (5)    \begin{equation*}  \theta_{1} := \theta_{1} - \alpha\frac{1}{m} \cdot \sum_{i=1}^{m}(h_{\theta}(x^{(i)}-y^{(i)})) \cdot x^{(i)} \end{equation*}

}

เมื่อทำการอัพเดทค่า \theta_{0} และ \theta_{1} ไปทีละstepเราก็จะเห็นได้ว่าระบบของเราพยายามจะหาค่าที่ j(\theta_{0},\theta_{1}) Cost funtion น้อยลงไปเรื่อยจนเกิดการลู่เข้า Convergence จนทำให้ได้ค่า Minimize ของระบบนั้นๆดังที่แสดงให้เห็นในรูป 3.4

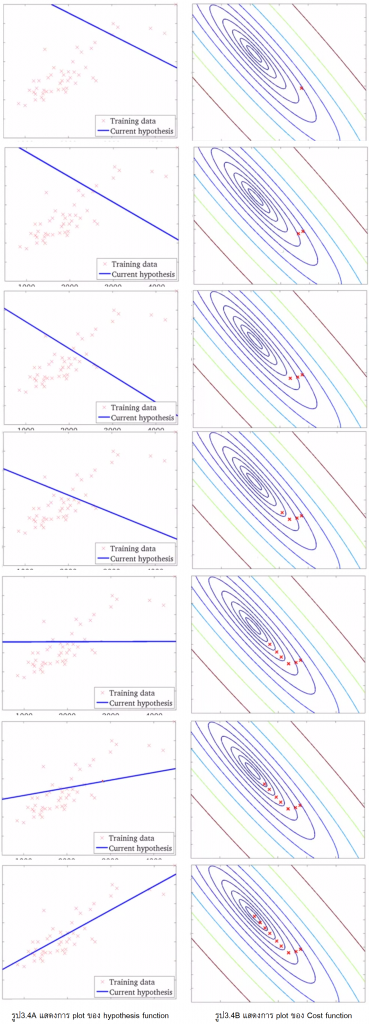
Multiple features (variables) with Gradient Descent

จากตัวอย่างข้างบนที่เรามีแค่ 1 ตัวแปรที่มีผลกับราคาบ้านก็คือขนาดพื้นที่ของบ้าน แล้วในกรณีที่เรามีตัวแปรมากกว่าหนึ่ง เช่น พื้นที่, จำนวนห้องนอน, จำนวนชั้น, อายุของบ้าน เป็นต้น (รูป 3.5) เราจะใช้อัลกอริทึม Gradient Descent ของเรากับข้อมูลของเราได้อย่างไร

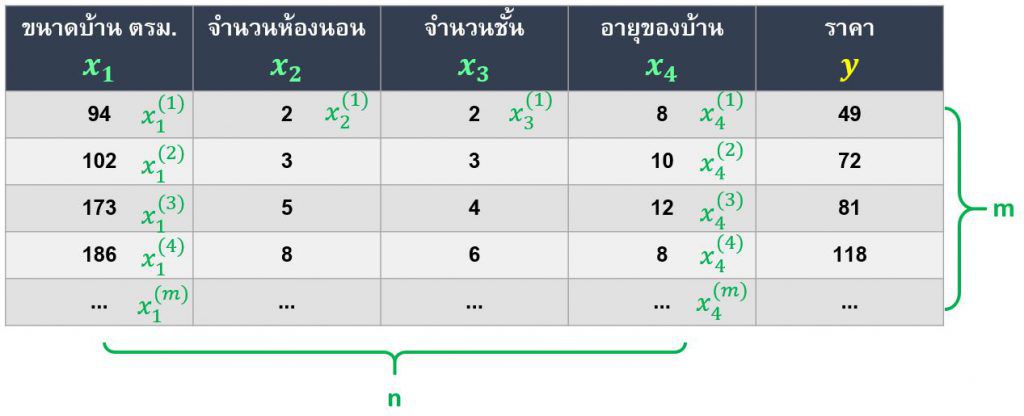
รูป 3.5 ตารางข้อมูลราคาบ้านตามตัวแปรมากกว่าหนึ่งตัว
จากสมการ Hypothesis ที่ใช้กับข้อมูล 1 ตัวแปร คือ 

 (6)    \begin{equation*}  h_{\theta}(x) = \theta_{0}+\theta_{1}x \end{equation*}

และเมื่อเรามีตัวแปรที่เพิ่มขึ้น indexค่า\theta ก็จะเพิ่มขึ้นตามจำนวนตัวแปรหรือตามจำนวน n ในตารางรูป 3.5 
เราสามารถเรียกสมการนี้ว่า "Multivariate Linear Regression"
ดังนั้น

 (7)    \begin{equation*}  h_{\theta}(x) & = \theta_{0}+\theta_{1}x_{1} +\theta_{2}x_{2}+\theta_{3}x_{3}+\theta_{4}x_{4} \\ & = \theta^{T}x \end{equation*}


เราก็จะได้สมการ h_{\theta}(x)ใหม่เพื่อเอาไปแทนในสมการ3.2 และ สมการ3.3 จะได้

Repeat Until Convergence {

 (8)    \begin{equation*}  \theta_{0} := \theta_{0} - \alpha\frac{1}{m} \cdot \sum_{i=1}^{m}(h_{\theta}(x^{(i)}-y^{(i)})) \cdot x_{0}^{(i)} \end{equation*}


 (9)    \begin{equation*}  \theta_{1} := \theta_{1} - \alpha\frac{1}{m} \cdot \sum_{i=1}^{m}(h_{\theta}(x^{(i)}-y^{(i)})) \cdot x_{1}^{(i)} \end{equation*}


 (10)    \begin{equation*}  \theta_{2} := \theta_{2} - \alpha\frac{1}{m} \cdot \sum_{i=1}^{m}(h_{\theta}(x^{(i)}-y^{(i)})) \cdot x_{2}^{(i)} \end{equation*}


 (11)    \begin{equation*}  ... \end{equation*}

}

สรุปจากบทความนี้เราได้ใช้ Gradient Descent algorithm เพื่อนำมาหา Minimize ของ Cost Function ในอัลกอริทึม Linear Regression โดยที่เราสามารถใช้ได้กับข้อมูลที่มีเพียง 1 ตัวแปรหรือ มากกว่า1ตัวแปร

มันส์ต้องแชร์
ไม่ใช่หนุ่มอักษรแต่อยากลองถ่ายทอดสิ่งที่ชอบผ่านตัวอักษร
Website http://drawasset.com

ใส่ความเห็น

อีเมลของคุณจะไม่แสดงให้คนอื่นเห็น ช่องข้อมูลจำเป็นถูกทำเครื่องหมาย *

Related Posts

Back To Top