“Linear Regression”
อัลกอริทึมแรกที่เราจะพูดถึงคือ Linear Regression ซึ่งเป็นหนึ่งในอัลกอริทึมของ “Supervised Learning” ที่ได้กล่าวถึงไปใน บทความ Machine Learning : ตอนที่ 1 ลองนึกภาพถ้าคุณมีบ้านที่ต้องการขายแต่ไม่รู้จะตั้งราคาที่เท่าไหร่ดีให้เหมาะสมกับท้องตลาด โดยราคาจะตั้งขึ้นจากขนาดพื้นที่ของบ้านตามข้อมูลกราฟ 2.1 ที่แสดงด้านล่าง
เมื่อคุณได้เห็นข้อมูลของราคาบ้านตามขนาดพื้นที่ของหลังอื่นก็คงพอจะนำมาเปรียบเทียบเพื่อกำหนดราคาขายบ้านของตัวเองได้ใช่มั้ยครับ เช่นในกรณีที่บ้านของคุณมีขนาด 200 ตรม. คุณก็อาจจะกำหนดราคาที่ 110 ล้านบาทเพื่อให้เหมาะสมกับท้องตลาด
ตัวละครใน Linear Regression
จากเรื่องการตั้งราคาบ้านเรามาคุยกันเรื่องตัวละครที่เราจะใช้เรียกในบทความนี้ ก่อนอื่นตาราง 2.1 คือข้อมูลที่เรามีที่แสดงราคาบ้านตามขนาดของพื้นที่บ้านที่ขายในท้องตลาด เราเรียกข้อมูลนี้ว่า “Training set” เป็นข้อมูลที่เราจะป้อนให้กับระบบเพื่อให้ระบบได้ทำการเรียนรู้
ตัวละครถัดมา “” คือจำนวนของ ข้อมูลใน Training set เช่นข้อมูลราคาบ้านที่เราหามาได้มี 117 หลัง เพราะฉนั้น
จึงเท่ากับ 117 สองตัว
จากข้อมูลที่เรามีถ้าผมลองถามว่าอะไรที่ส่งผลต่อราคาบ้านในท้องตลาด อะไรที่เป็นตัวแปร”อินพุท” ที่ทำให้ราคาบ้านเปลี่ยน…. ใช่ครับ ขนาดของบ้านก็คือตัวแปรอินพุท และราคาตามข้อมูลคือตัวแปรเอาท์พุทครับและละครอีกสองตัวที่ผมจะใช้คือ ““และ “
” ซึ่ง
เราจะให้หมายถึงตัวแปรอินพุท(ขนาดพื้นที่ของบ้าน) และ
หมายถึงตัวแปร เอาท์พุท(ราคาบ้าน) ในกรณีที่ผมเรียก หนึ่งตัวอย่างของ Training set ผมจะใช้
โดยเราจะเรียกว่า “Training sample” หรือให้เห็นภาพชัดขึ้นเช่น ขนาดของบ้าน 102 ตรม จะราคาเท่ากับ 72 ล้านบาท (102,72) คือ
จากตรงนี้
และ
ไม่ได้ยกกำลัง สอง แต่เป็นตำแหน่งของข้อมูล Training sample ใน Training set ของเรา เพราะฉนั้น
ก็คือตำแหน่งของข้อมูลครับ
จากที่เราได้ลองประเมิณราคาบ้านจากข้อมูล (Training set) ที่เราได้มาเรานำ Training set มาผ่าน “Learning Algorithm” ที่ทำให้ระบบได้เรียนข้อมูลที่เราป้อนให้ ซึ่งหลังจากนั้นเราก็จะสามารถประเมิณราคาบ้านโดยป้อนอินพุทใหม่ซึ่งในกรณีนี้คือขนาดพื้นที่บ้านของเราที่ต้องการจะตั้งราคาให้กับ“Hypothesis” หรือ การตั้งสมมุติฐาน และเมื่อผ่านการตั้งสมมุติฐานแล้ว เราก็จะได้เอาท์พุทซึ่งเป็นราคาบ้านเราที่ต้องการให้เหมาะสมกับตลาดที่ได้แสดงโมเดลไว้ที่รูป 2.3 เดี๋ยวเราจะมาลงรายละเอียดในเรื่อง Hypothesis กันต่อในบทความนี้ครับ
Hypothesis
ในรูป 2.4 แสดงข้อมูลราคาบ้านตามพื้นที่ขนาดของบ้านก็คงพอทำให้เราเห็นกราฟ“เส้นตรง”ที่ลากผ่านกลุ่มกากบาทซึ่งเป้าหมายของเราคือการเลือกตำแหน่งที่เส้นจะลากไปหรือการหาค่าของ ที่เหมาะสมที่สุดเพื่อทำให้เส้นสีฟ้าของเราใกล้กับกากบาทให้มากที่สุดเพื่อให้การตั้งราคาของเราเหมาะสมที่สุดกับตลาด แล้วอะไรคือ
??
จากสมาการ ซึ่งความชันของกราฟเส้นตรงนี้จะขึ้นอยู่กับค่า
และเส้นจะตัดแกน
ที่
เช่นในกรณีนี้
มีค่าเท่ากับศูนย์ คำถามคือ แล้วเราจะเลือกค่า
และ
ได้อย่างไร ก่อนอื่นเราจะมาทำความเข้าใจกันว่าถ้าค่า
และ
เปลี่ยนไปแล้วกราฟเส้นตรงของเราจะรูปร่างหน้าตาเป็นอย่างไร หลายท่านที่คุ้นเคยกับสมการเส้นตรงนี้อยู่แล้วก็สามารถข้ามได้เลยครับ
เริ่มจากลองคิดดูว่าเมื่อ กราฟควรจะออกมาเป็นแบบไหนระหว่าง (A) และ (B)
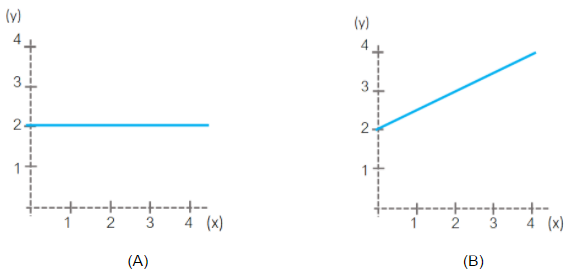
ใช่ครับและคำตอบก็คือ (A) ข้อสังเกตุคือเมื่อ ที่คูณกับ
และ
ของเราก็จะมีค่าคงที่ ที่เท่ากับ
หรือให้อธิบายอีกอย่างคือเมื่อเราลองแทน
ลงใน
ดังนั้น
ตลอดในทุกช่วงของ
Cost Function
ย้อนกลับไปที่เป้าหมายของเราคือหาค่า ,
ที่เหมาะที่สุดเพื่อให้ได้เส้น Hypothesis ของเราออกมาสอดคล้องหรือ “Fit” กับ training set ของเรามากที่สุด โดยเราสามารถใช้สมการที่เรียกว่า “Cost Function” หรือ เรียกอีกอย่างว่า “Squared error function”(สมการ 2.1) โดยนำมาครอบบน
ก็คือ Hypothesis (สมการ 2.2) เพื่อที่จะได้หาตำแหน่งของเส้นที่ใกล้ที่สุดกับกากบาทสีแดงที่เป็น Training set จากตัวอย่างในรูป 2.4 ถ้าพูดให้เข้าใจง่ายขึ้นก็คือ สมการนี้พยายามหาค่าของ
,
ที่ทำห้ค่า error ต่ำที่สุด
และ
แล้วเราจะทราบได้อย่างไรว่าค่า ,
ที่เราใช้เหมาะสมที่สุดแล้ว ในตัวอย่างที่แสดงในรูป 2.6 คำตอบคือเราต้องหาค่าที่
ต่ำที่สุด หรือเราจะเรียกว่า “minimize
” เท่าที่เส้นฟังก์ชั่น
จะใกล้กับ Training set ทุกตัว เราลองมาดูตัวอย่างเพื่อให้เห็นภาพชัดเจนยิ่งขึ้นครับ ที่กราฟฟังก์ชั่น
(รูป2.6A) เราจะพบกากบาทสีแดง 3 จุดก็คือ Training set และเส้น Hypothesis ที่ลากผ่านและไม่ผ่าน Training set ของเรา คำถามคือเส้นที่ฟังก์ชั่น
เท่ากับเท่าไหร่ที่ Hypothesis หรือ
มีค่าเหมาะสมกับ Training set เรามากที่สุดคือ จากตัวอย่างนี้เราจะมาเริ่มที่ระบบของเรามีค่า
ดังนั้นเราก็เพียงสนใจแต่การหาค่าที่
เมื่อ แทนลงในสมการที่ 2.1 จะได้ผลลัพท์ของเส้น Hypothesis ออกมาผ่านจุดกากบาท (Training set) โดยมีค่าความแตกต่างในแนวแกน
ระหว่างจุดบนเส้นที่ผ่านกากบาทเท่ากับศูนย์
(1) 
ต่อไปลองเปลี่ยนค่า , เมื่อ
แทนลงในสมการที่ 2.1 จะได้ผลลัพท์ดังนี้
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} j(\theta_{1}) & = \frac{1}{(2)(3)}[(0.5-1)^2+(1-2)^2+(1.5-3)^2] \\ & = \frac{1}{(2)(3)}(3.5) \\ & = \frac{3.5}{6} \simeq 5.83 \end{split} \end{equation*}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%20373%20129'%3E%3C/svg%3E)
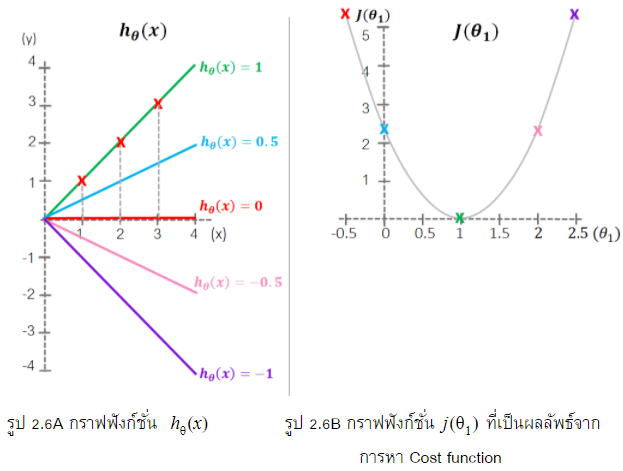
จากรูปที่ 2.6A แสดงผลลัพท์จากการหา ซึ่งแทนด้วย -1, -0.5, 0, 0.5, 1 และเมื่อเราplotค่าoutputลงในกราฟรูป2.6B เราสามารถเห็นภาพได้อย่างชัดเจนจากรูป 2.6B ว่าค่าที่
ที่ต่ำที่สุด
จะเท่ากับ 1 โดยที่ค่า
มีค่าเท่ากับศูนย์
แล้วในกรณีที่ต้องคำนวณสองตัวแปรหล่ะ จากรูปที่ 2.7 เมื่อเราสนใจแค่ตัวแปรเดียว เราจะสามารถสนใจแค่ค่า หรือ
รูปเป็นเส้นโค้งก็สามารถเข้าใจได้ แต่เมื่อเราต้องคำนวนทั้งสองตัวแปร การหาค่า Minimize
นั้นจะมีความสัมพันธ์ของทั้ง
และ
และ ค่าผลลัพท์ของ
ด้วย เพื่อให้เห็นภาพชัดเจนรูป 2.7 ของเราแสดงภาพ Contour plot ของสมการ 2 ตัวแปรเพื่อ ให้เห็นว่าจุดที่ต่ำที่สุด “Global optimal” ว่าอยู่ตำแหน่งใด
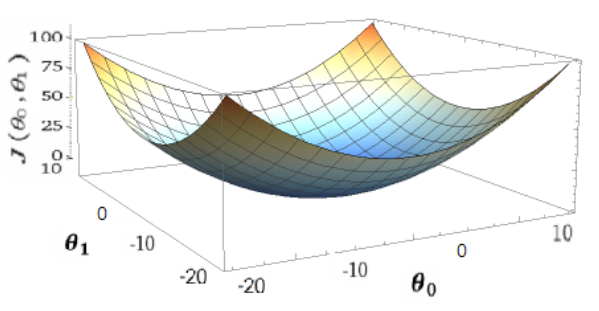
จาก Contour line (รูป 2.8B) ลองมองในมุมจากข้างบนลงบนแแอ่ง (Top view) จะเห็นเส้นวงกลมทับซ้อนกันในแกนของ และ
ซึ่งทุกจุดบนเส้นหนึ่งเส้นมีค่าเท่ากัน ถ้าบางท่านที่สงสัยว่ากากบาทสามอันที่เรียงกันอันบนสุดอยู่ใกล้จุดกึ่งกลางมากที่สุดแต่ทำไมถึงมีค่าเท่ากัน ถ้าย้อนกลับไปที่รูป 2.7 กากบาทสามจุดนั้นมี”ความสูง”ที่เท่ากันเมื่อเทียบจากจุดที่ลึกที่สุดนั่นเองครับ
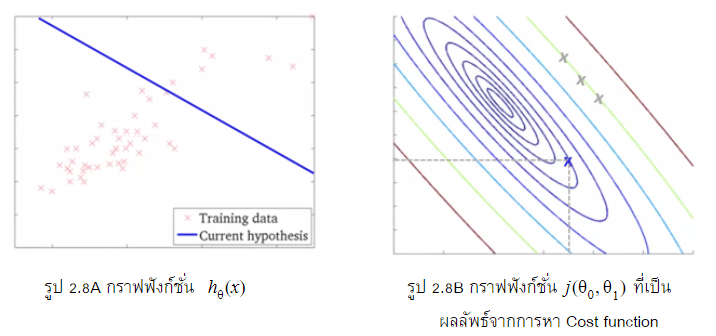
โดยที่แน่นอนว่าเป้าหมายของเราคือต้องหาจุดที่ต่ำที่สุดในระบบโดย ที่เปลี่ยน ก็จะส่งผลถึงเส้นทิศทางของ Hypothesis ของเราครับ
สรุปเนื้อหาในบทความนี้
จากเนื้อหาของบทนี้คงทำให้ผู้อ่านเห็นภาพของการหา Hyppthesis จากอัลกอลิทึม Linear Regression และลักษณะ Training set แบบไหนที่เราสามารถใช้ Linear Regression ได้ และในบทนี้ได้กล่าวถึงตัวแปรและสมการสำคัญอาทิเช่น Cost function และ Square error Function
ในบทความถัดไปเราจะมาหาวิธีหาค่า Minimize Cost function โดยวิธีที่เรียกว่า “Gradient Descent” ที่เราจะได้ใช้กันในบทความถัดไป Machine Learning : ตอนที่ 3

![Rendered by QuickLaTeX.com \[j(\theta_{0},\theta_{1}) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}-y^{(i)}))^{2}............................................(2.1)\]](https://www.blogmun.com/wp-content/ql-cache/quicklatex.com-1ef7e762ba4ca429fe86cacf4cd3ff9f_l3.png)
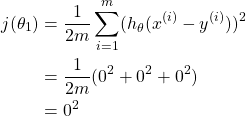
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} j(\theta_{1}) & = \frac{1}{(2)(3)}[(0.5-1)^2+(1-2)^2+(1.5-3)^2] \\ & = \frac{1}{(2)(3)}(3.5) \\ & = \frac{3.5}{6} \simeq 5.83 \end{split} \end{equation*}](https://www.blogmun.com/wp-content/ql-cache/quicklatex.com-6f21a5747009b1ff596531dcabcb4587_l3.png)